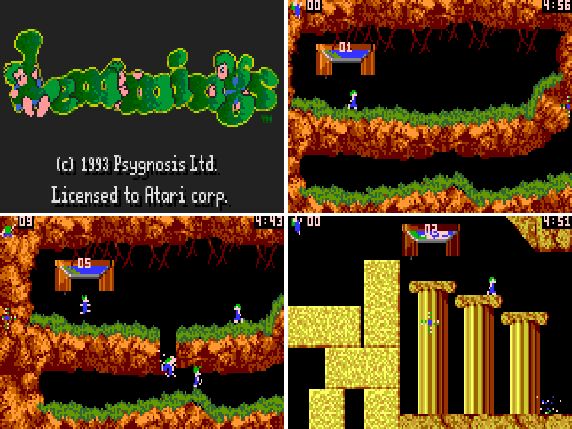
 A Lemmings egy logikai, puzzle típusú számítógép játék, a DMA Design (manapság Rockstar North) cég fejlesztette, és 1991-ben a Psygnosis gondozásában jelent meg. Mike Dailly tervezte a játékot, amit később sokféle platformra adaptáltak (pl. Commodore Amiga), sokunk talán az MS-DOS verzióra emlékezhetünk.
A Lemmings egy logikai, puzzle típusú számítógép játék, a DMA Design (manapság Rockstar North) cég fejlesztette, és 1991-ben a Psygnosis gondozásában jelent meg. Mike Dailly tervezte a játékot, amit később sokféle platformra adaptáltak (pl. Commodore Amiga), sokunk talán az MS-DOS verzióra emlékezhetünk.
Akiknek új a cím, kiváltképp tartsanak velünk, kihagyhatatlan.
A játék során egyre nehezedő pályákon kell bizonyítani. A pályák lehetnek egy képernyősek, vagy ha nagyobbak, lehet gördíteni a képet.
A feladatod, hogy a bejárattól, a kijáratig (minél több) lemminget oda navigálj. A tervező abból indult ki, hogy a lemminget a valóságban is így viselkednek, hiszen vakon követik a többieket, még ha előreláthatóan is veszélyes a művelet... Tehát, a lemmingek elkezdenek potyogni a bejáratnál, és neked mint parancsnoknak meg kell mondanod mit csináljanak.
 A képernyő alján keresd a pályán elérhető műveleteket. Az első két gomb, a lemmingek érkezésének sebességét csökkenti valamint növeli. Hasznos, de csak akkor, ha már tudod, hogy sikerülni fog egy pálya.
A képernyő alján keresd a pályán elérhető műveleteket. Az első két gomb, a lemmingek érkezésének sebességét csökkenti valamint növeli. Hasznos, de csak akkor, ha már tudod, hogy sikerülni fog egy pálya.
A többi művelet csak korlátozott számban áll rendelkezésedre, és ez teljesen pályafüggő. Kattints egy ikonra, majd egy lemmingre. Pontosan azt fogja csinálni, amire megkérted: elkezd ásni, lépcsőt épít, vagy akár fel is robban :( Erre azért van szükség, mert van olyan eszköz, amivel egy lemmingből "útzár" lesz. Nem engedi tovább a többi lemminget - a többiek biztonsága érdekében. Miután mindenkit kimenekítettél addig nincs vége a pályának amíg lemming van rajta. Kvázi elkerülhetetlen...
A pályák grafikai megvalósítása elsőrangú az összes platformon, és ez alól még a DOS verzió (vga) sem kivétel! A pályák szinte minden esetben teljesen egyedi elemekből épülnek fel, és mindig más a feladat. Apró eltérések persze lehetnek, az adott hardware limitációi miatt. Íme egy lista mi mindenen találkozhatsz vele:
- 3DO
- Acom Archimedes
- Amstrad CPC
- Apple IIgs
- Macintosh
- Atari Lynx
- Commodore 64
- Amiga CD32
- CDTV
- MS-DOS
- SNES
- GameBoy
- Sega Game Gear (és Genesis)
- Windows
- TurboGrafx-CD
 A pályákat ráadásul időre kell megoldani, és pályától függően valamely százaléknyi lemminget kell legalább a kijárathoz eljuttatni.
A pályákat ráadásul időre kell megoldani, és pályától függően valamely százaléknyi lemminget kell legalább a kijárathoz eljuttatni.
A lemmingek ügyesek, tudnak mászni, ásni, építeni, rombolni... Vannak helyek ahol csak egyféle megoldás létezik. Gondold át mindig mi lehet a legjobb stratégia.
Minden pálya után kapsz egy kódot, amit a menüben meg tudsz adni, és onnan tudod folytatni a játékot.
Folytatások
- Xmas Lemmings
- Oh No! More Lemmings
- Lemmings 2: The Tribes
- 3D Lemmings
- Lemmings Revolution
A fejlesztése sem volt mindennapi, Dave Jones beszámolója szerint a játék azt hivatott bizonyítani eleinte, hogy lehet jópofa animált karaktereket rajzolni 8x8 pixeles maximum sprite mérettel. Ráadásul a pályaszerkesztő a Deluxe Paint koncepciójára lett megtervezve, így mindenki képes volt pályát készíteni a vállalaton belül. Sőt, igazi versengések voltak, ki tud nehezebbet tervezni. :)
Videó
Online Játék
Csalások
Pályakódok
Írd be az alábbi kódok valmelyikét hogy egy adott pályától kezdhesd a játékot (FUN értékelés).
| Pálya | Kód |
|---|---|
| 1 | - |
| 2 | IJJLDNCCCN |
| 3 | NJLDLCADCY |
| 4 | HNLHCIOECW |
| 5 | LDLCAJNFCK |
| 6 | DLCIJNLGCT |
| 7 | LCANLLDHCO |
| 8 | CINNLDLICJ |
| 9 | CEKHMDLJCO |
| 10 | MJHMDLCKCW |
| 11 | OJOLHCGLCO |
| 12 | HMDLCIOMCJ |
| 13 | MDLCAKLNCS |
| 14 | DLCIJNMOCM |
| 15 | LCANNMDPCJ |
| 16 | CINNMDLQCS |
| 17 | CAKHLFLBDU |
| 18 | IJJLNHCCDS |
| 19 | NJNNHCADDR |
| 20 | HLFLCMNEDW |
| 21 | LNHCAKNFDS |
| 22 | FLCMKLLGDJ |
| 23 | LCAOLLFHDS |
| 24 | CIOLLFLIDL |
| 25 | CEJHOFHJDO |
| 26 | OKHMFLCKDM |
| 27 | NJMFLCALDU |
| 28 | HMNHCIOMDQ |
| 29 | ONHCAKNNDN |
| 30 | FHCMKLMODO |
A fejlesztők kitaláltak egy játék specifikus kódot, így feleslegessé vált a játékmentés. Ha kiváncsi vagy hogy épül fel egy kód olvass tovább.
A kód tíz számjegyből áll: 0123456789
0 A pontos szerepe ismeretlen
123456 A megmentett lemingek %-a az előző pályán
78 pálya
9 ellenőrző érték (checksum)
Az ellenőrző értéket a következő egyenlettel lehet kiszámítani (ahol a code(N) függvény egy ASCII karakter értéke az N pozíción):
code(9) = 74 + (sum(code(0)..code(8)) modulus 16)
Példa
IJJLDNCCC?
? = 74 + ((73 + 74 + 74 + 76 + 68 + 78 + 67 + 67 + 67) modulus 16)
? = 74 + (644 modulus 16)
? = 74 + 4
? = 78
N = 78
Tehát a fenti példának az ellenőrző értéke (?) az N karakter lesz.